Author Archives: Glen Whitney

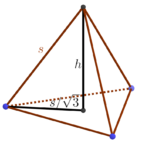
This post just takes care of some of the calculations used in planning the Golden Gate STEM Fair event. First, the plan was to make the structure shown at the right: a regular tetrahedron on top of a regular octahedron. Moreover, the resulting construction was intended to be five meters tall. Hence, the question arises: How long should each truss of the structure be to achieve the desired height?

It’s easier to work in the other direction. Assume that each edge of the structure has length s; how tall is the overall structure? Let’s start with the tetrahedron part. The apex lies directly over the center of the equilateral triangular base of the tetrahedron. We know the side length of the that triangle is s so we use the formula relating the radius r of a circle and the side of an inscribed regular polygon: s = 2rsin τ/2n, where n is the number of sides of the regular polygon, in this case three (and τ is the full circle constant, equal to 2π). So we get sin τ/6 = sin 60°, which is √3/2, from which we conclude that s = √3 r or r = s/√3.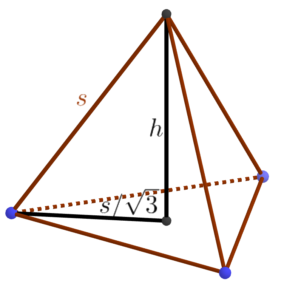

Now we have a right triangle from the base of the tetrahedron to its apex, from which we conclude that h = √(s²-s²/3) = s√2/√3.

That tells us the height of the tetrahedron on top, but what about the octahedral base? We could go through a similar sort of calculation, albeit more involved, but we can also save ourselves a lot of trouble by noticing that if we lay the whole structure down on its side, we get a tetrahedron nestled up against the side of an octahedron, which makes it clear that the regular octahedron and regular tetrahedron are the same height. Thus, the tower overall has height s2√2/√3. Solving this for s when the height is 500 centimeters yields about 306 cm. And since we’re using boxes measured in inches and a foot is about 30cm, it’s easiest to think of that as 10 feet. So the moral of the story is that we need each truss to be ten feet long.

How many boxes will that take? Well, the boxes are 6 inches on a side, but they lie on the trusses along a face diagonal, which is 6√2 or about 8.5″. So we need the trusses to be 120/8.5 = 14.1 boxes long, or say 15 boxes long to be on the safe side. Extending a truss by one unit typically takes four boxes (one on the top and bottom and two in the middle), so that’s roughly 60 boxes per truss. With 15 trusses in the whole structure (just by counting in the diagram at the top), we can estimate about 900 boxes in the entire structure. And we know that’s an overestimate, because the trusses overlap each other where they join. So it’s a safe number to use for planning.

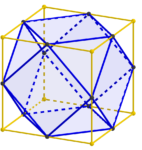
In the last MathStream post, we concluded that if you took spheres with holes at the points indicated by black dots in the diagram below, you could connect them with struts to form a lattice composed of alternating octahedra and tetrahedra.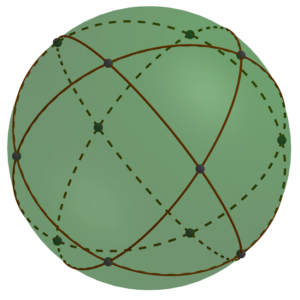

But for building large-scale constructions, we’d like something comprised of components that are a little easier to make or obtain. The goal of this post is to show how that same oct-tet lattice can be constructed simply from cubical boxes.

The first step is to notice that we could shrink the struts to be as short as we like, or even do away with them altogether. If we had a whole lot of spheres just touching (or rather, glued together) at the black spots, they would form an oct-tet lattice.

But spheres are a bit hard to work with. Instead of thinking of them as points on a sphere, instead connect those same twelve points with straight lines and planar faces:

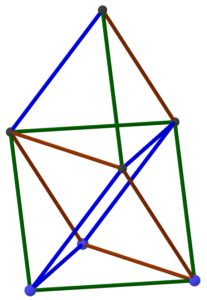
That produces a shape called a cuboctahedron, and what we have established is that cuboctahedra joined vertex-to-vertex form an oct-tet lattice.

But where do cuboctahedra come from? If we read much of the way down the Wikipedia page, we see the statement that “a cuboctahedron is a rectified cube.” Unraveling that word “rectified,” this statement just means that if you start with a cube, take the midpoint of every edge, and then connect the new points when the edges they correspond to connect, you get a cuboctahedron. Or we can “undo” the rectfication and re-create the cube from the cuboctahedron we have.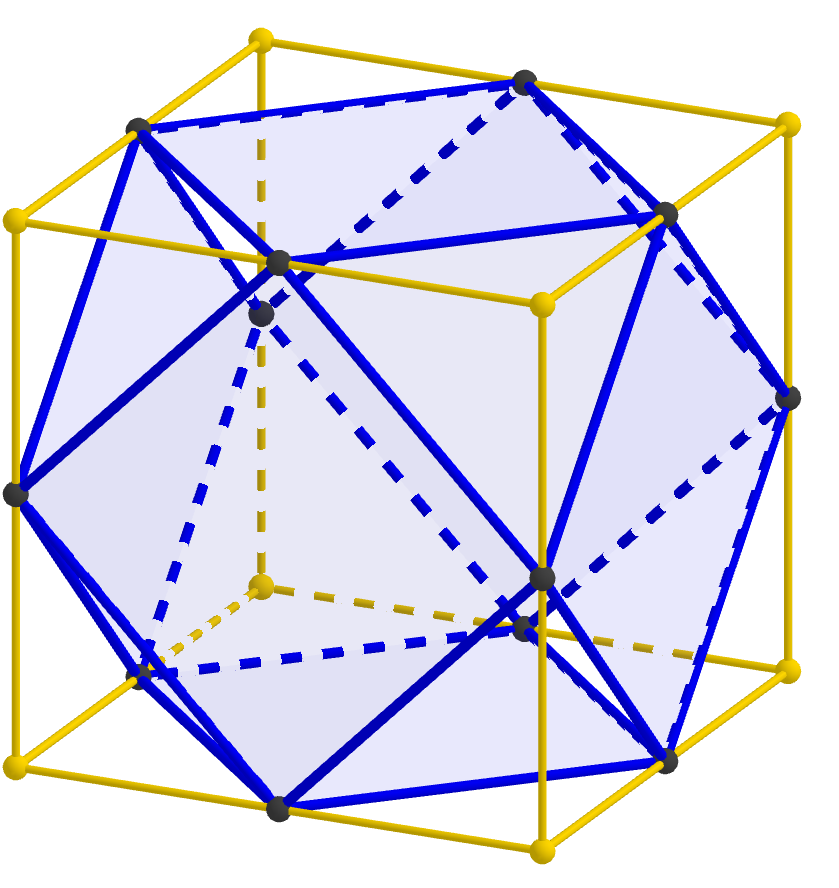

Therefore, connecting cuboctahedra vertex-to-vertex is the same as connecting cubes edge-to-edge, so we have established that cubes joined edge-to-edge form an oct-tet lattice. We’ve taken enough steps that this statement may now seem a bit mysterious, but hopefully this final image will help tie the whole thing together; notice that each strut in the oct-tet lattice passes through the midpoint of an edge of the cube.

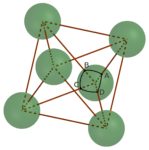
The ease with which we could draw an equilateral triangle on the sphere naturally leads to wondering whether other constructions work out so nicely. For example, can we construct the square of points that would be needed to locate the holes for building a regular octahedron from styrofoam balls and sticks?

Since the central angle between any two adjacent vertices of the square is again τ/6 = 60°, the sides of the square are the same length as the triangle’s sides in the previous construction. So let’s just look up the geometric construction of a square and use that on the sphere. Unfortunately, you immediately hit a snag: the first step is to “extend the line segment PQ.” And I don’t know of a really practical way to extend line segments on a sphere. You could try a flexible ruler, but it’s hard to get it lined up and to draw with it in place. Or you can make three equilateral triangles that all share the same vertex; then the side of the third one extends the original one. That’s fine in theory, but in practice it’s a lot of work and it’s easy for small errors to accumulate, leaving the sum of the three angles meeting at the vertex a bit different from 180° = τ/2.

So to make things much easier, we will use a special property of this particular square. As you can see in the picture, the regular octahedron can also be viewed as a square bipyramid. That tells us that the central angle between points A and C diagonally opposite on the square we want is τ/4 = 90°. And that in turn means that the diagonal of the square on the surface of the sphere is exactly 1.5 times as long as the side of the square. Contrast this to the situation of a square in the plane, where the diagonal is the much more computationally difficult √2 times the side of the square, but beware! This relationship does not hold for all squares on the surface of a sphere. Indeed, the ratio of diagonal to side length of spherical squares ranges from √2 to 2, and in fact, you can determine the side length of a spherical square from just that ratio (and the radius of the sphere).

But for the particular square we want, we do have this lovely relationship that the diagonal is 1.5 times the length of the side, and so we can find the other two corners just as we did for the equilateral triangle, simply using a thread of length d for one arc and 1.5d for the other arc. So building a regular octahedron should also be quite feasible.

We can go a bit further than this. If you play around with constructing these squares and triangles, you will find that alternating them completely covers the sphere.

In other words, there are just twelve points on the surface of the sphere so that each one is a vertex of two equilateral triangles and two squares, alternating. That’s a pretty special structure, and it allows the existence of a very strong framework filling space called the oct-tet lattice consisting of alternating octahedra and tetrahedra.

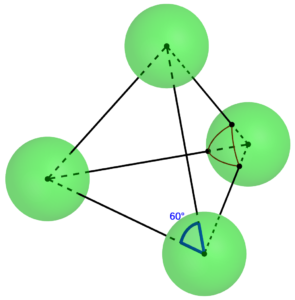For this project, I needed to figure out (a) where should the holes be in spheres to connect them by straight lines to form a regular tetrahedron, and (b) how to locate those points on a physical sphere. The diagram makes part (a) fairly straightforward. We can see that the angle between any two holes (as viewed from the center of one of the spheres) should be 60°, the angle at each vertex of an equilateral triangle. And since 60° is one-sixth of a full circle (or an angle of τ/6, as the tauists point out), we can find the required distance d between any two holes on the surface of a sphere of radius r to be d = rτ/6, or approximately d ≈ 1.047r.

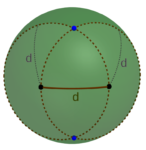
Now, how should we actually locate the points? As you can see from the diagram, they form a sort of “spherical equilateral triangle,” each point the same distance from each of the other two. And as you may recall, it’s pretty easy to construct an equilateral triangle in the plane. Fortunately, exactly the same procedure works on a sphere: First, select any two points a distance d apart on the sphere. Then using each of the two points as center, trace out a spherical circle with radius d on the surface of the sphere. (In practice, you only need a small section of each circle in the vicinity of where they’re going to intersect.) Each of the two points at which those two circles intersect represents one of the two possible locations for the third vertex of the desired triangle.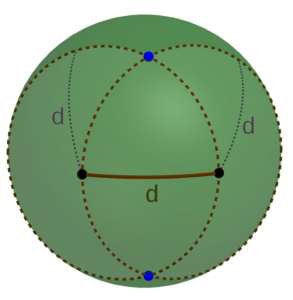
Moreover, it’s easy to perform this construction in practice. And mathematical curiosity makes us wonder: if it works for triangles, will it work for other constructions as well?