Category Archives: MakeStream

the heart of Studio Infinity, MakeStream articles show structures – and frequently how to make them – that exhibit interesting design ideas, often inspired by mathematics.

10 Jan

Announcing the Prisms of Eight Free Build

If you’re in the Seattle area, Studio Infinity and the Seattle Universal Math Museum will be hosting a freestyle build on Saturday, January 11th. We have absolutely no clue what this structure will look like when complete and would love for you to be part of the team that plans and executes its construction!

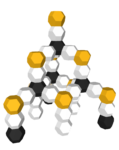
The unit we will be building with is a regular octahedral junction with eight triangular prismatic “arms” protruding from its faces:

We have a few ideas for what this building unit might be good for, but we are far more excited to see what a group of creative math enthusiasts can dream up.

The build will take place on Saturday, January 11th from 9:00am to 12:00pm in the 4th floor exhibit hall of the Seattle Convention Center. While the Joint Math Meetings have a registration fee the rest of the week, entry to the exhibit hall is completely free this Saturday. There will be many cool mathy things in the exhibit hall for both children and adults to enjoy, so bring friends and family of all ages!

06 Jan

Diamond Lattice Tower Practice Build

In preparation for the announced JMM build, we worked out some kinks this past weekend with a practice build.

Since the final structure is just shy of 17 feet tall, it was important to have a venue with high ceilings. The Seattle Universal Math Museum has an ongoing partnership with the Georgetown Steam Plant, who generously offered their boiler room. (For fun, you can use their virtual tour to navigate yourself to the boiler room, as featured in the photos below.)

Read More →
06 Jan

Announcing the Diamond Lattice Tower

On Wednesday, 2025 January 8th at the Joint Mathematics Meetings in Seattle, Studio Infinity will be facilitating a group build using Giant Octablocks. If you follow our projects, you might recognize them as the trunctated octahedra from the TOWARD build at Harvey Mudd College or from a freestyle build at Open Sauce 2024. This time we will be leveraging the fact that the hexagonal faces of the blocks are at the perfect angles to build within a diamond cubic crystal structure if we restrict ourselves to a subset of four of them per block. The end goal — a Diamond Lattice Tower:

Read More →
18 Jul

Studio Infinity + You

Are you interested in bringing a mathematical art installation to your school or community? Studio Infinity would love to help!

Mathematical art has the power to inspire and educate. Installing a large work as a group helps foster or reinforce a sense of community around shared intellectual and artistic interests. And it can provide an opportunity for people to engage with and think about math in ways they may never have before.

Read More →
18 Mar

Planning TOWARD

Because TOs Work As a RD, Studio Infinity’s next project has officially been dubbed TOWARD! We are collaborating with Peter Kagey, a Visiting Assistant Professor of Mathematics at Harvey Mudd College, who found the TO particularly appealing due to its double life as a permutohedron. The build will take place at Harvey Mudd College, so we’re opting to use Harvey Mudd’s black, white, and gold as our palette. Here’s our poster for the event, featuring a digital mock-up of what we intend to build:

Read More →