An Oct-Tet of Cubes

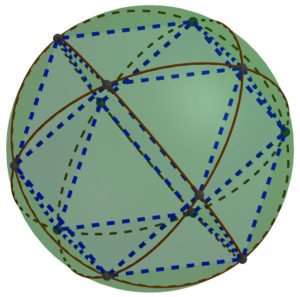
In the last MathStream post, we concluded that if you took spheres with holes at the points indicated by black dots in the diagram below, you could connect them with struts to form a lattice composed of alternating octahedra and tetrahedra.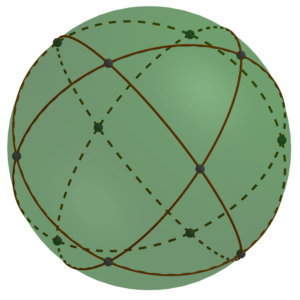

But for building large-scale constructions, we’d like something comprised of components that are a little easier to make or obtain. The goal of this post is to show how that same oct-tet lattice can be constructed simply from cubical boxes.

The first step is to notice that we could shrink the struts to be as short as we like, or even do away with them altogether. If we had a whole lot of spheres just touching (or rather, glued together) at the black spots, they would form an oct-tet lattice.

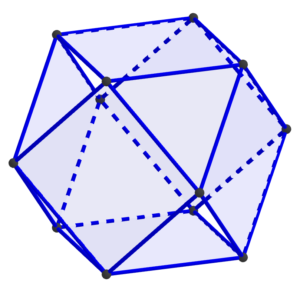
But spheres are a bit hard to work with. Instead of thinking of them as points on a sphere, instead connect those same twelve points with straight lines and planar faces:

That produces a shape called a cuboctahedron, and what we have established is that cuboctahedra joined vertex-to-vertex form an oct-tet lattice.

But where do cuboctahedra come from? If we read much of the way down the Wikipedia page, we see the statement that “a cuboctahedron is a rectified cube.” Unraveling that word “rectified,” this statement just means that if you start with a cube, take the midpoint of every edge, and then connect the new points when the edges they correspond to connect, you get a cuboctahedron. Or we can “undo” the rectfication and re-create the cube from the cuboctahedron we have.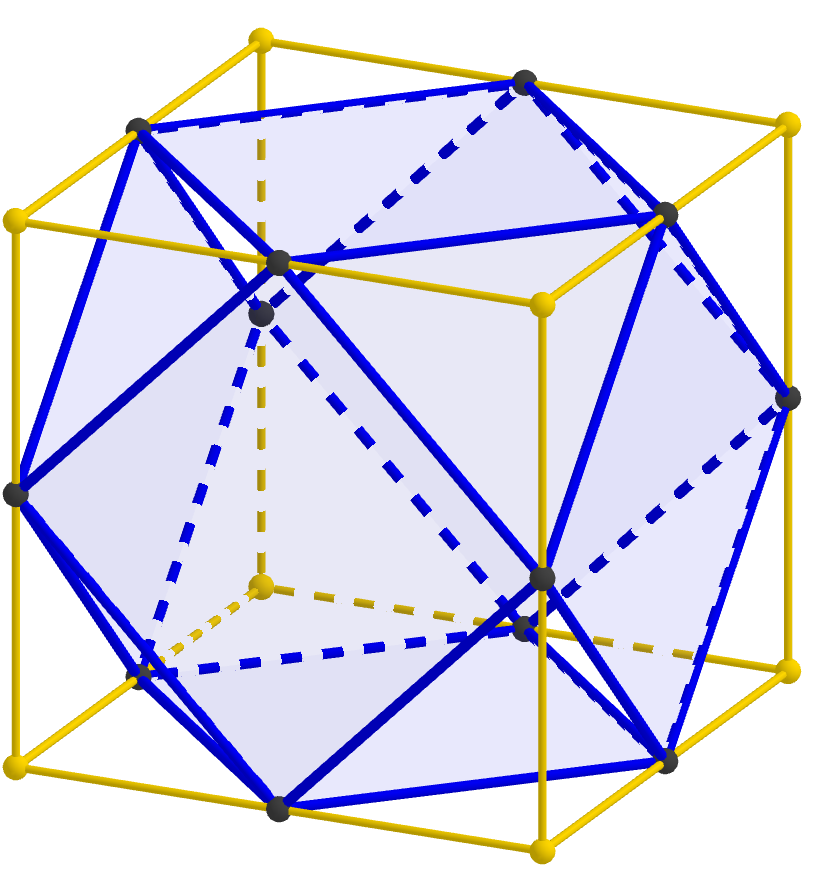

Therefore, connecting cuboctahedra vertex-to-vertex is the same as connecting cubes edge-to-edge, so we have established that cubes joined edge-to-edge form an oct-tet lattice. We’ve taken enough steps that this statement may now seem a bit mysterious, but hopefully this final image will help tie the whole thing together; notice that each strut in the oct-tet lattice passes through the midpoint of an edge of the cube.