GGSF: Calculations
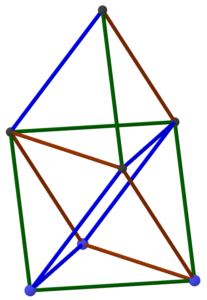This post just takes care of some of the calculations used in planning the Golden Gate STEM Fair event. First, the plan was to make the structure shown at the right: a regular tetrahedron on top of a regular octahedron. Moreover, the resulting construction was intended to be five meters tall. Hence, the question arises: How long should each truss of the structure be to achieve the desired height?
It’s easier to work in the other direction. Assume that each edge of the structure has length s; how tall is the overall structure? Let’s start with the tetrahedron part. The apex lies directly over the center of the equilateral triangular base of the tetrahedron. We know the side length of the that triangle is s so we use the formula relating the radius r of a circle and the side of an inscribed regular polygon: s = 2rsin τ/2n, where n is the number of sides of the regular polygon, in this case three (and τ is the full circle constant, equal to 2π). So we get sin τ/6 = sin 60°, which is √3/2, from which we conclude that s = √3 r or r = s/√3.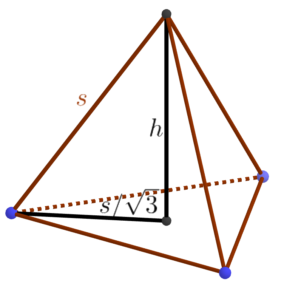
Now we have a right triangle from the base of the tetrahedron to its apex, from which we conclude that h = √(s²-s²/3) = s√2/√3.
That tells us the height of the tetrahedron on top, but what about the octahedral base? We could go through a similar sort of calculation, albeit more involved, but we can also save ourselves a lot of trouble by noticing that if we lay the whole structure down on its side, we get a tetrahedron nestled up against the side of an octahedron, which makes it clear that the regular octahedron and regular tetrahedron are the same height. Thus, the tower overall has height s2√2/√3. Solving this for s when the height is 500 centimeters yields about 306 cm. And since we’re using boxes measured in inches and a foot is about 30cm, it’s easiest to think of that as 10 feet. So the moral of the story is that we need each truss to be ten feet long.
How many boxes will that take? Well, the boxes are 6 inches on a side, but they lie on the trusses along a face diagonal, which is 6√2 or about 8.5″. So we need the trusses to be 120/8.5 = 14.1 boxes long, or say 15 boxes long to be on the safe side. Extending a truss by one unit typically takes four boxes (one on the top and bottom and two in the middle), so that’s roughly 60 boxes per truss. With 15 trusses in the whole structure (just by counting in the diagram at the top), we can estimate about 900 boxes in the entire structure. And we know that’s an overestimate, because the trusses overlap each other where they join. So it’s a safe number to use for planning.