Rhombic Dodecahedra from Truncated Octahedra

Studio Infinity has long been interested in builds consisting of polyhedra as modular units. Even better if the structure ends up being another recognizable polyhedron, like when we used regular dodecahedra to construct the skeleton of a rhombic triacontahedron in the DodecaRT build. Analogously with the DodecaRT build, it turns out that the geometry of the truncated octahedron (TO)

is just right so that, by gluing units face-to-face, we can obtain the skeleton of a rhombic dodecahedron (RD).

The motivating observation was that TOs can be used to form rhombus-like loops. If you take the centroids of the corner units of such a loop, you’ll find that the rhombus determined by those four points has a long-diagonal to short-diagonal ratio of $\sqrt{2}$ to $1$, which is precisely the rhombus that makes up the faces of the rhombic dodecahedron.

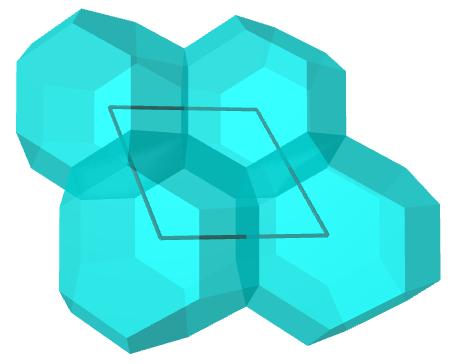
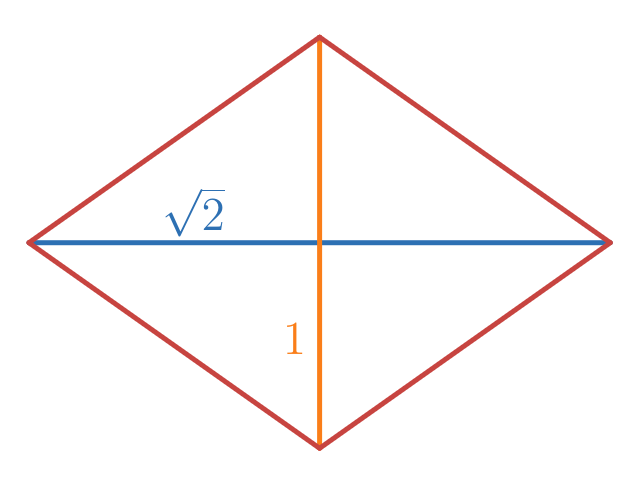
If you elongate the edges of this rhombus by adding the same number of TOs between vertices, you end up with a similar $\sqrt{2}$-rhombus, which means there is an easy way to scale the build by adding more TOs:

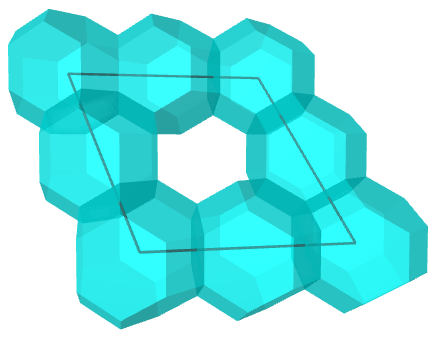
A RD has two types of vertices: degree-3 vertices, where three rhombi meet at their obtuse angles, and degree-4 vertices, where four rhombi meet at their acute angles. Crucially, the geometry of the TO also accommodates these incidences.

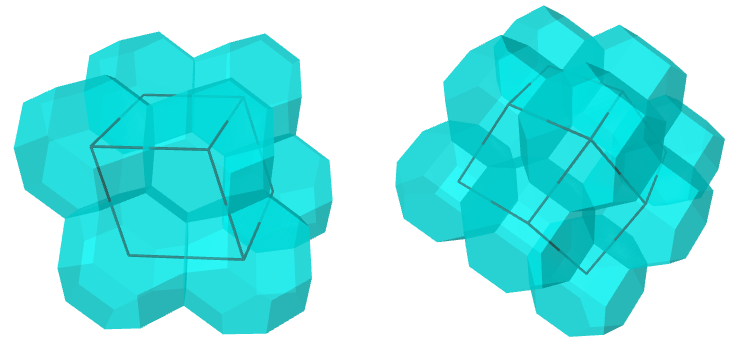
At some point in the near future, we would like to try building this RD of TOs. Since we’d want to do it in a way that makes the features of the RD “pop,” there are two good candidates. We could use one TO per edge

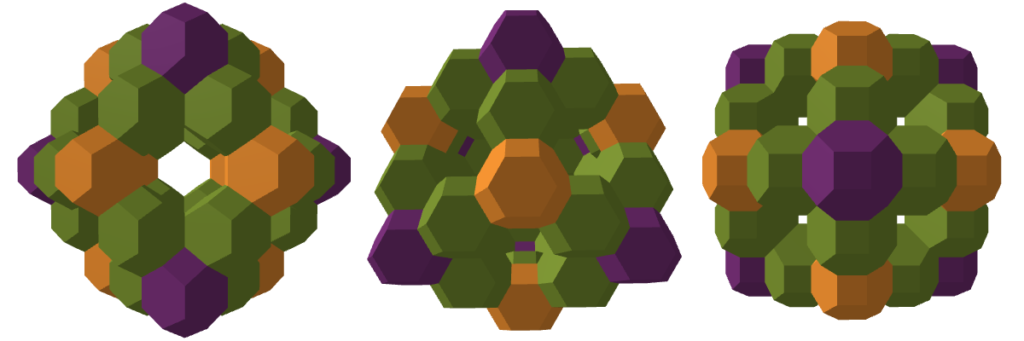
or two TOs per edge

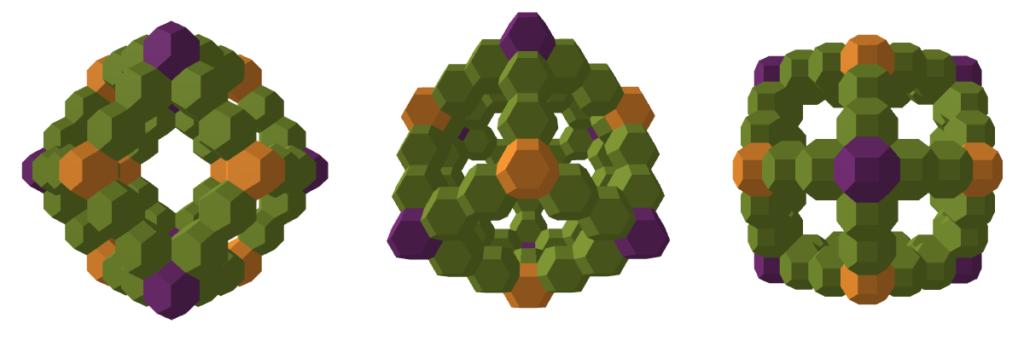
as illustrated in our fiscal sponsor SUMM‘s palette. Pending material selection and an engineering review, we’ll probably “go big” with the latter, and that way also have the option to build the smaller version down the road. Stay tuned!