Truncated Triakis Tetrahedron
For the actual building event mentioned in the previous post (linked above), participants could choose from a variety of target polyhedra. The origami inspiration was the PHiZZ unit, which stands for Pentgons Hexagons in Zig Zag, so the ideal targets consist of just pentagons and hexagons. With Euler’s formula for polyhedra and a little calculation you can determine that such a shape must have exactly twelve pentagons and almost any number of hexagons; the page for the event includes a table of candidates.
| Materials |
|---|
| 42 modular units cut out and folded (see Modular Origami, without the origami) (preferably 9 each of four colors and 6 of another) |
I chose the Truncated Triakis Tetrahedron as my target: (not only because of the alliteration, it’s a nice size and has pleasing symmetry that breaks the building down into four simple, identical sub-assemblies)

To assemble this, I worked from a diagram of the edges, graciously colorized by Elliot Kienzle:
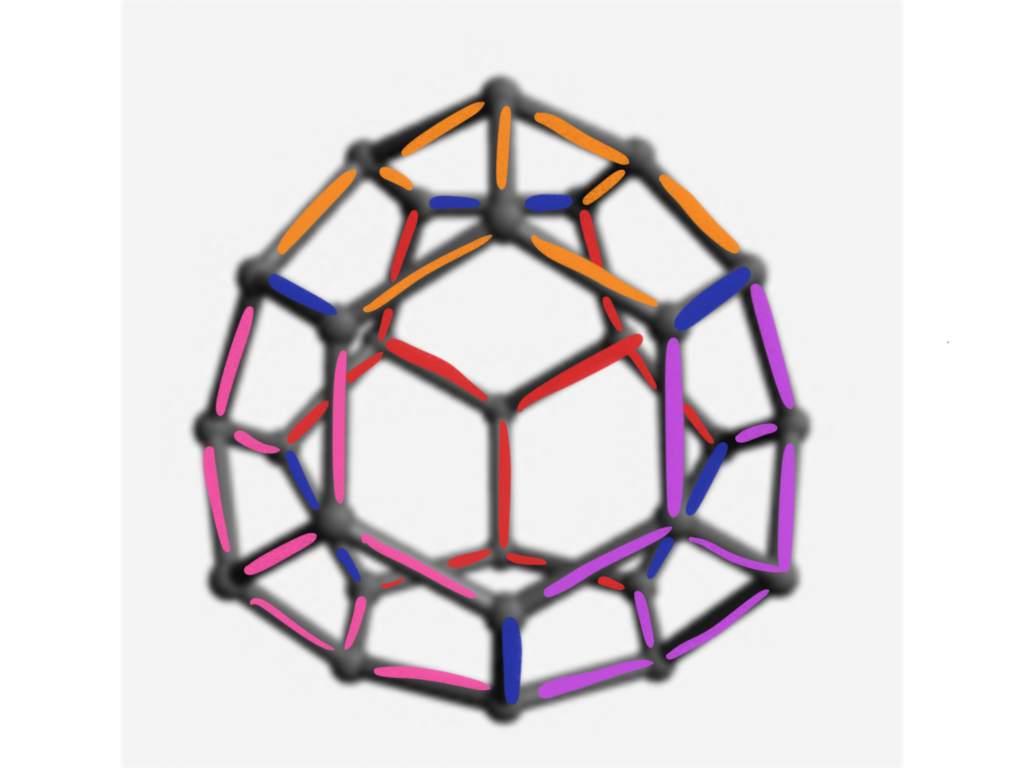
I found it easiest to start by making each of the lighter-colored sections. They’re all the same, made of nine pieces each. You make one three-way connection all the same color (as shown in the previous post), and then turn each of the three opposite ends of each of these pieces into a three-way connection, like so:

Repeat with the other three colors.
When you have your four sub-assemblies, you can connect two neighboring loose ends of one color with corresponding loose ends of another color at the two ends of a new unit of the darker color. Here are the components laid out schematically to show how they go together:

And here they are overlapped in the actual way the first trio of connections will be made:

And here they are once both ends of the blue unit have been fully connected:

This process of connecting sub-assemblies with one additional unit happens in six places, shown by the blue edges in Elliot’s diagram above. (These six edges are actually the remnants of the six original edges of the tetrahedron that the truncated triakis tetrahedron is based on.) Once you’ve made all those links, everything hangs together like so:

(Note that this image is shown from the same perspective as Elliott’s diagram above, used as the construction guide.)
Participants took this basic concept in a variety of directions, and here’s a mini-gallery of some of the results:







