A Late-Entry Lattice: The Surprising Rigid Honeycomb

A couple speakers dropping out at the last minute left a hole in the Math & Art session’s schedule the other week at MAA MathFest 2024 in Indianapolis, IN. As the famous expression you’ve no doubt heard countless times goes: when life gives you cancellations, make cantellations!

The session’s organizer, David Richeson, asked Studio Infinity if there were any good last-minute group activities. We had iterated the boxtet building system several times by now, and the materials are cheap and readily available, so this seemed like the ideal candidate to fill the breach. We’d just need to find a bunch of identical, inexpensive boxes, and plan on using pipe cleaners along the diagonals of the boxes’ small faces, similarly to this method used before.

Previously, we had used boxtets to build a “cuboxtahedron,” a cuboctahedron with boxes for square faces and open triangular faces:

The idea this time was to use the third dimension of the boxes to realize a honeycomb lattice involving cubes and cuboctahedra.

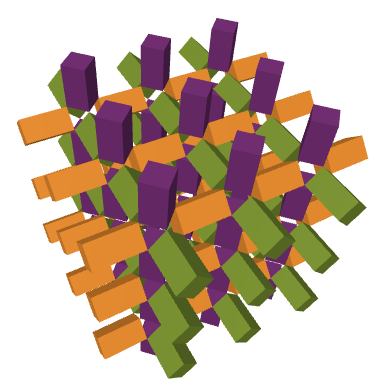
The natural candidate was the cantellated cubic honeycomb, a space-filling arrangement of cubes, cuboctahedra, and rhombicuboctahedra. Here you can see how these shapes are arranged to fill space together, peeled back a layer at a time:

If we remove the cuboctahedra (red) and rhombicuboctahedra (dark green), we are left with an arrangement for our boxes. Here are a couple renderings at different scales:

Since the cuboxtahedron construction is rigid and every joint where boxes come together in the above construction is a cuboxtahedron, this structure is also rigid! This might be surprising, since the boxes take up relatively little space.

While the diagrams above show cubes, it turns out that this construction works for any rectangular box! For an $a \times b \times c$ box, pick any two of the dimensions (say, $a$ and $b$), and then create an irregular cuboxtahedron with six $a \times b$ rectangular faces (instead of square), four equilateral triangle windows of edge length $a$, and four equilateral triangle windows of edge length $b$. Here is what an irregular cuboxtahedral junction might look like:

Since any box dimensions would work, we scouted stores in the Indianapolis area. We ended up at Box Co in Carmel, IN, and after some discussion with the proprietor, found that they had hundreds of surplus $6″ \times 6″ \times 12″$ boxes from a previous canceled order. These boxes were fortuitously in the ideal range for building a human-scale construction, and the square bases would make the junctions nice, regular cuboctahedra. So we settled on a mutually agreeable price for a few hundred, and set back off to MathFest for the activity.

Here’s a rendering of the lattice pattern we would end up with in theory:

Here are some snapshots of the build, from wrangling boxes and pipe cleaners to assembly:

The finished construction (Prof. Annalisa Crannell, one of the session speakers, posed with Surprising Rigid Honeycomb for scale):

Not bad for a build we only learned we’d be facilitating at 9:00 pm the night before!

And if you’ve been squinting hard enough at our photos, you just might have noticed our fiscal sponsor, the Seattle Universal Math Museum, whose flexibility made this last-minute operation possible. Thanks, SUMM!