Space Unboxed
Our recent honeycomb lattice build at MathFest took up relatively little space for how rigid it was, so a natural question is what proportion of space the boxes take up in an infinitely repeating lattice. Since the boxes are themselves empty, a more amusing framing might be: how much of space would be boxed versus unboxed?
In our construction, we used boxes of dimension $a \times a \times b$. The way we thought about filling space with these boxes in their lattice arrangement was by complementing them with cuboctahedra with edges of length $a$ and irregular rhombicuboctahedron with $8$ equilateral triangular faces of edge length $a$, $6$ square faces of edge length $b$, and $12$ rectangular $a \times b$ faces:


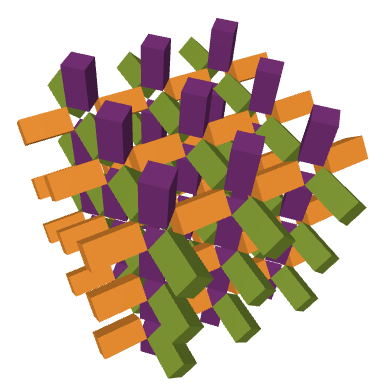
From this perspective, the space occupied by these cuboctahedra and rhombicuboctahedra is the unboxed space.
To get a sense of how little space the boxes contain, we can look at the smallest cube containing our irregular rhombicuboctahedron. If we look at what else that cube contains from the honeycomb, we’ll see it’s $8$ eighth-cuboctahedra and $12$ quarter-boxes.

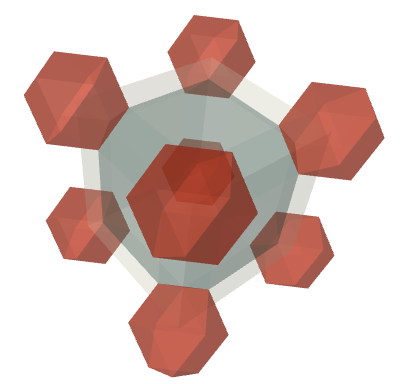

In other words,
$$V_{\textrm{cube}} = V_{\textrm{rhombicuboctahedron}} + V_{\textrm{cuboctahedron}} + 3V_{\textrm{box}}$$
We know $V_{\textrm{box}} = a^2 b$ and can show that
$$V_{\textrm{cube}} = (\sqrt{2} a + b)^3$$
Since we can recreate the cantellated cubic honeycomb by arranging these cubes in a simple cubic honeycomb, the fraction of space taken up by the boxes is
$$\rho = \frac{3V_{\textrm{box}}}{V_{\textrm{cube}}} = \frac{3 a^2 b}{(\sqrt{2} a + b)^3}$$
When we have cubic boxes and $b = a$, this reduces to
$$\rho = \frac{3}{(1+\sqrt{2})^3} \approx 0.2132$$
In other words, the sculpture repeated ad infinitum would leave about $78.68$ percent of space unboxed if the boxes were cubes.
Our boxes were $6″ \times 6″ \times 12″$, which is an $a:b$ ratio of $1:2$. This gives
$$\rho = \frac{6}{(2+\sqrt{2})^3} \approx 0.1508$$
and leaves a whopping $84.92$ percent of space unboxed! Since
$$\lim_{b \rightarrow \infty }\frac{3 a^2 b}{(\sqrt{2} a + b)^3} = 0$$
we could box as arbitrarily small a ratio of space as we like by choosing $b$ much, much greater than $a$.

