Trees of Willow, True Love, and Tiling

Trees of Willow, True Love, and Tiling

Mai Nguyen

Math 168: Making Math Material

I’ve been eating off these plates ever since I can remember. No matter how many beautiful or interesting pieces of dishware in our family’s house, I always gravitate towards the “Willow Plate” design.

My mom told me the story of the plate even before I started school: a high-ranking court lady and a low-ranking servant boy fell in love and wanted to get married, but could not due to the social hierarchy and control of her family. Eventually, they ran away from the altar where she was meant to marry someone else, escaping on boat to an abandoned island. Her father, furious, searched for them and eventually found out where they were. In desperation, the couple prayed to the spirits, who transformed them into a pair of love birds, and they were able to fly away together.

In the process of researching this lead, my inner Asian pride in the legacy of this beautiful blue-white design was shot down. The origins of the “Willow Plate” are in 18th century chinoiserie, plateware created and designed by Europeans inspired by China’s rich culture. So, not quite the authentic, Asian-pride narrative I’d hoped for. In any case, the plate leaves lots of imagination for mathematical exploration.

On the surface, the use of concentric circles can be outlined to create the plate. Although the Willow Plate design is very versatile and used on many patterns, the circular dish is most popular. I personally see the story with a distinct beginning-middle-end as a cycle of sorts. The use of concentric circles to outline the designs and create the eventual fluted shape and full plate emphasizes this.

Although the conception of the story’s meaning is simply a synthesis of European impressions of Chinese culture in the 18th century, the passing on of the story has transformed from a marketing gimmick to a point of connection at the dinner table for families and beyond.

In authentic Chinese pottery, geometric patterns and re-imaginations of nature are key points as well, but less as decoration and more to create a larger piece of nature.

 

In this plate, especially on the rim and outer sections, there is also symmetry by rotation. Around the rim of the plate, the patterns form small grids, bounded by the separate sections of the plate. Among them are many named tile patterns and others that I’ll describe myself, going from top to bottom:

• Columns of a circle within a circle
• Rows of a square within a square
• Rows of a circle within square on the left
• Ring of 6 trapezoids with curved sides and a hole cut out in the middle
• Ring with inscribed superellipse
  • A superellipse is a closed curve contained within a triangle, resembling a curve-sided diamond
  • In this case, the resulting superellipse will look like a 4-pointed star with curved edges
  • The equation of a superellipse as  in the Cartesian form
• 4-Petaled Flowers
  • petals inscribed with lines through vertices
  • The section between the flowers is, as above, a super ellipse with a factor of n (0,1), with a circle in the middle

Each of these patterns, when repeated, is used to fill up the plane. A tessellation refers to the filling up of a planar space with geometric shapes as a pattern, without gaps or overlap When the geometric pattern can be slid a finite distance and superimposed over itself, the tiling is periodic. Each of the cases above is periodic.

 

By contrast, an aperiodic tiling is one that cannot be slid a finite distance and be superimposed on itself. The Penrose tiling is a classic example. 

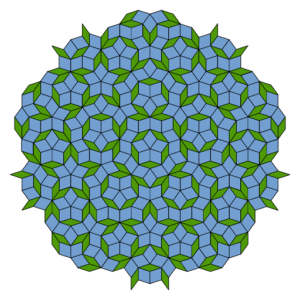
Sir Roger Penrose(1931-), an English mathematician whom the tiling is named after, became interested in tessellations mainly because of the artist M. C. Escher’s early works, exploring the possibilities of math and physics through art in finite space. A famous example of Escher’s work is the Devil’s Angel; in it, you can see similar concepts of a repeating pattern, a tile, filling up a space infinitely.

Fascinatingly, the golden ratio, φ (Greek letter “phi”), a special number = (1+√5)/2, ~1.618 and appearing many times often unexpectedly in geometry, art, etc., shows up here in rhombuses of the Penrose Tiling. One way to describe the golden ratio is that when you divide a quantity into 2 unequal parts, the ratio of the whole length over the longer length is equal to the ratio of the longer length over the shorter length.

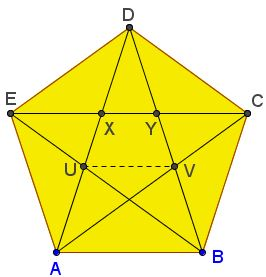
In a regular pentagon, if you draw diagonals across the polygon, the ratio of the side length to the any line segment congruent to line segment EX will be φ (ex. line segment DE/ line segment EX= φ).

The obtuse triangle in the figure at left is congruent to half of the red rhombus in a Penrose tiling, and the acute triangle is congruent to half of the yellow rhombus. Thus, the construction utilizes the relationship of the sides of the tiles and φ.

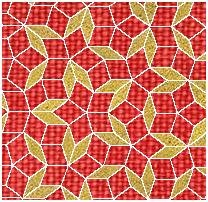
Designs similar to the Penrose Tiling have been created in the past. For one, physicist Peter J. Lu of Harvard University claims that the quasicrystal, an ordered but not periodic structure, form of the Islamic “girih”, a geometric art form, has been found to very closely resemble the Penrose Tiling. While the design on the Darb-i  Imam shrine wall, built in 1453, is not completely perfect, it may be reminiscent of the Penrose Tiling. At the same time, the use of geometry to convey the perfection of God suits the golden ratio and its intrinsic beauty.

While the Willow Plate design does not utilize the Penrose Tiling, clearly there was geometric intent behind the use of tiling segments and symmetry. While the European makers created their own story and geometric imprints, the legacy of this type of dishware will always be associated with China. While history itself can be seen as linear and neatly chronological, my exploration of these plates was anything but. Similarly, any topic and idea in math can always be explored on a deeper level. When considering the existing foundation of knowledge, I continue to have the same sense of wonder at the never-ending paths for exploration in art and math alike.  I imagine that even the oldest civilizations felt the same way.

 

Sources and Acknowledgements:

“Cosmology, Escher and the Field of Screams.” In The Dark: A blog about the Universe, and all that surrounds it. Accessed October 3, 2018. https://telescoper.wordpress.com/2012/03/20/cosmology-escher-and-the-field-of-screams/.

Cut the Knot. “Golden Ratio in Regular Pentagon.” Cut the Knot. Accessed October 3, 2018. http://www.cut-the-knot.org/do_you_know/GoldenRatioInRegularPentagon.shtm. 

Google. “Blue and white porcelain bowl.” Google Arts and Culture. Accessed October 3, 2018. https://artsandculture.google.com/asset/blue-and-white-porcelain-bowl-with-landscape-izushi-ware/tAH1cc4-0EVE9Q. 

Johnston, Hamish. “Islamic ‘quasicrystals’ predate Penrose tiles.” PhysicsWorld. Accessed October 3, 2018. https://physicsworld.com/a/islamic-quasicrystals-predate-penrose-tiles/.

Meisner, Gary. “Penrose Tiling and Phi.” The Golden Number. Last modified May 13, 2012. Accessed October 3, 2018. https://www.goldennumber.net/penrose-tiling/. 

Wikipedia. “Penrose Tiling.” Wikipedia. Accessed October 3, 2018. https://en.wikipedia.org/wiki/Penrose_tiling.

———. “Tessellation.” Wikipedia. Accessed October 3, 2018. https://en.wikipedia.org/wiki/Tessellation.