Three-D Pythagorean Theorem

This recent post described a construction that demonstrated the “Three-D Pythagorean Theorem.” Here we dive a bit deeper into this bit of mathematics that may be less familiar than it deserves.

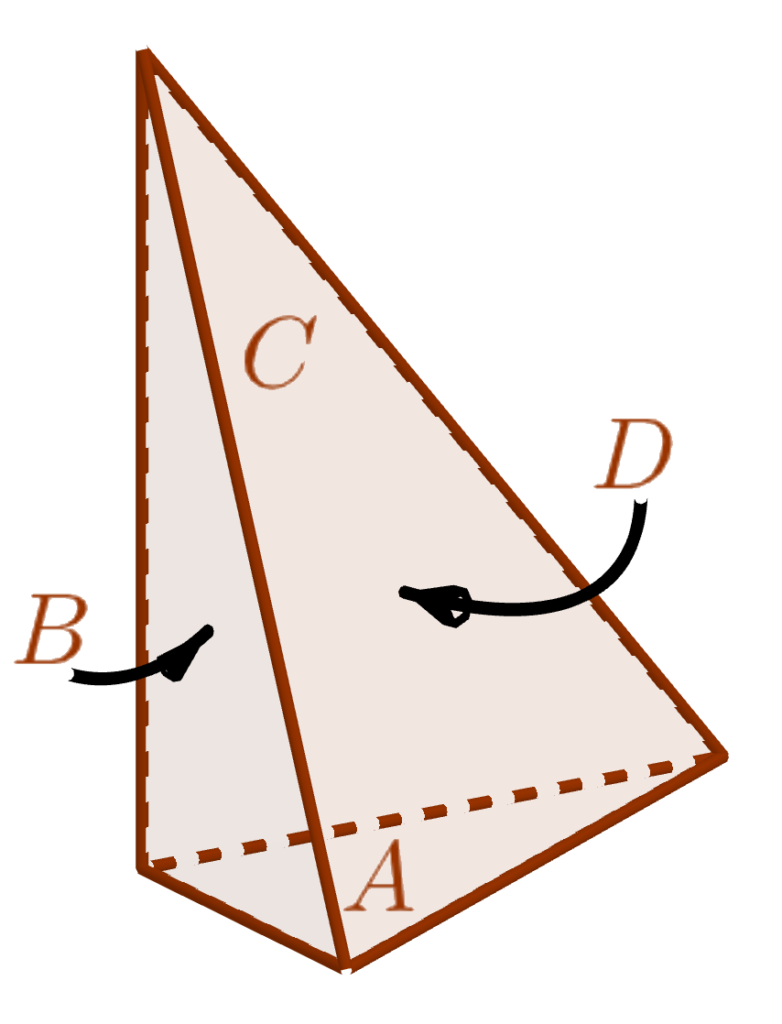
A right tetrahedron has, by definition, a vertex where three right angles meet (there can be only one). An example is shown in the diagram at right. Suppose that the areas of its faces are $A < B < C < D$. Then the Three-Dimensional Pythagorean Theorem (also known as de Gua’s Theorem) says that \[A^2 + B^2 + C^2 = D^2.\]

This is a generalization of the “usual” two-dimensional Pythagorean Theorem. How so? Here we say that one theorem “generalizes” another if it has the other theorem as a special case. How can we get the 2D theorem as a special case of the 3D? Unlike with most generalizations, it’s not particularly clear.

In fact, I was only able to derive the usual PT from the 3D one if I also presumed the special case case of the usual PT that the diagonal of a square is √2 times its side — but that case is quite simple to prove on its own, by considering a 2-by-2 grid of squares and four of the diagonals of squares in that grid that themselves form a square (you can see essentially the full proof to the left).

Now, assuming the 3D Pythagorean Theorem and the fact that the diagonal of a square is √2 times its side, we derive the usual Pythagorean Theorem as follows: Let $a$ and $b$ be arbitrary lengths, and consider the right tetrahedron with legs (edges meeting at the right-angle vertex) of lengths $a$, $b$, and $b$.

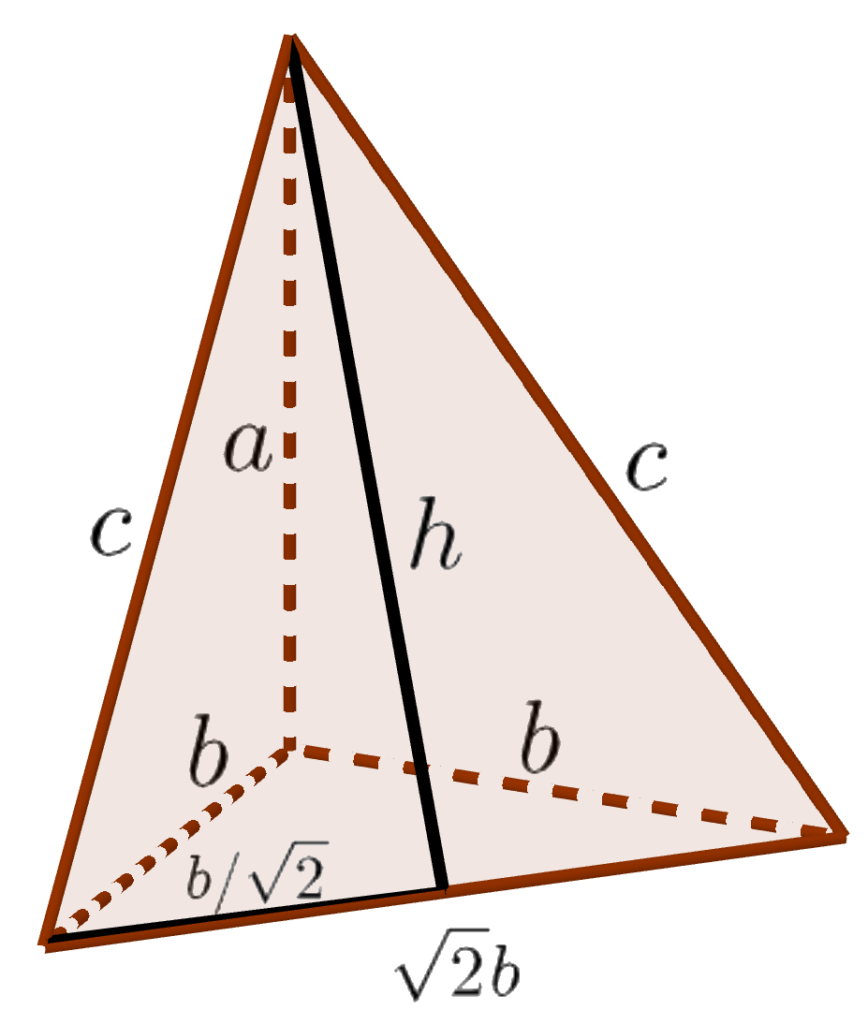
Then the edges of the base (the face that does not include the right-angle vertex) of this right tetrahedron are $c$, $c$, and $\sqrt{2}b$, where $c$ is the hypotenuse of a right triangle with sides $a$ and $b$ (see the diagram at right). The areas of the other three faces are $ab/2$, $ab/2$, and $b^2/2$. Hence, by the 3D PT, the area of the base is $b^2(2a^2 + b^2)/4$, and so the height $h$ of the base (from the vertex between the two sides of length $c$) is $\sqrt{a^2 +b^2/2}$. But the altitude of an isosceles triangle bisects the third side, so $c$ is also the hypotenuse of a right triangle with legs $b/\sqrt2$ and $\sqrt{a^2+b^2/2}$.

Iterating this construction, we see that $c$ must also be the hypotenuse of a right triangle with legs $b/2$ and $\sqrt{a^2+3b^2/4}$. Iterating further, $c$ must also be the hypotenuse of a right triangle with legs $b/4$ and $\sqrt{a^2+15b^2/16}$, and further in general $c$ is the hypotenuse of a right triangle with legs $b/2^n$ and $\sqrt{a^2 + b^2(2^{2n}-1)/2^{2n}}$. Taking the limit as $n$ grows without bound, $b/2^n$ approaches zero and $(2^{2n}-1)/2^{2n}$ approaches one, and we see that $c$ must equal $\sqrt{a^2+b^2}$, as desired.

Of course, one would never really prove the usual Pythagorean Theorem in this way; the above merely serves to justify calling the 3D PT a “generalization” of the usual one, in that we can recover the usual one from it.

All this begs the question, how do we prove the Three-D Pythagorean Theorem itself? The simplest way is to generalize the following atypical “proof” of the usual Pythagorean Theorem:

Place a right triangle with legs $a$ and $b$ on a coordinate plane so that the vertex of its right angle is at the origin and the legs extend along the $x$ and $y$ axes, respectively. Then by the two-intercept form of a line, the equation of the line containing the hypotenuse is $x/a + y/b = 1$. Also, the line through the origin given by $y=ax/b$ is perpendicular to the hypotenuse (see the diagram to the left, with the hypotenuse in blue). These two lines intersect at the point $(ab^2/(b^2+a^2), a^2b/(b^2+a^2))$. The line segment from the origin to this point (dark green in the diagram) has length $ab/\sqrt{a^2+b^2}$. But this line segment is also an altitude of the right triangle with respect to the hypotenuse as base. Since the area of the rectangle is $ab/2$, by dividing we get that the hypotenuse of the right triangle must be $\sqrt{a^2+b^2}$.

I put “proof” in quotes because it’s circular — I actually used the Pythagorean Theorem to get the length of the altitude segment. However, if we do the same proof in three dimensions, we still only need the ordinary Pythagorean Theorem to get the length of the corresponding segment, and so we get a bona fide proof of the 3D Pythagorean Theorem (using the usual PT, which is OK because as mentioned, we would not actually use the 3D PT to prove the usual 2D PT — there are plenty of independent proofs). That goes like so:

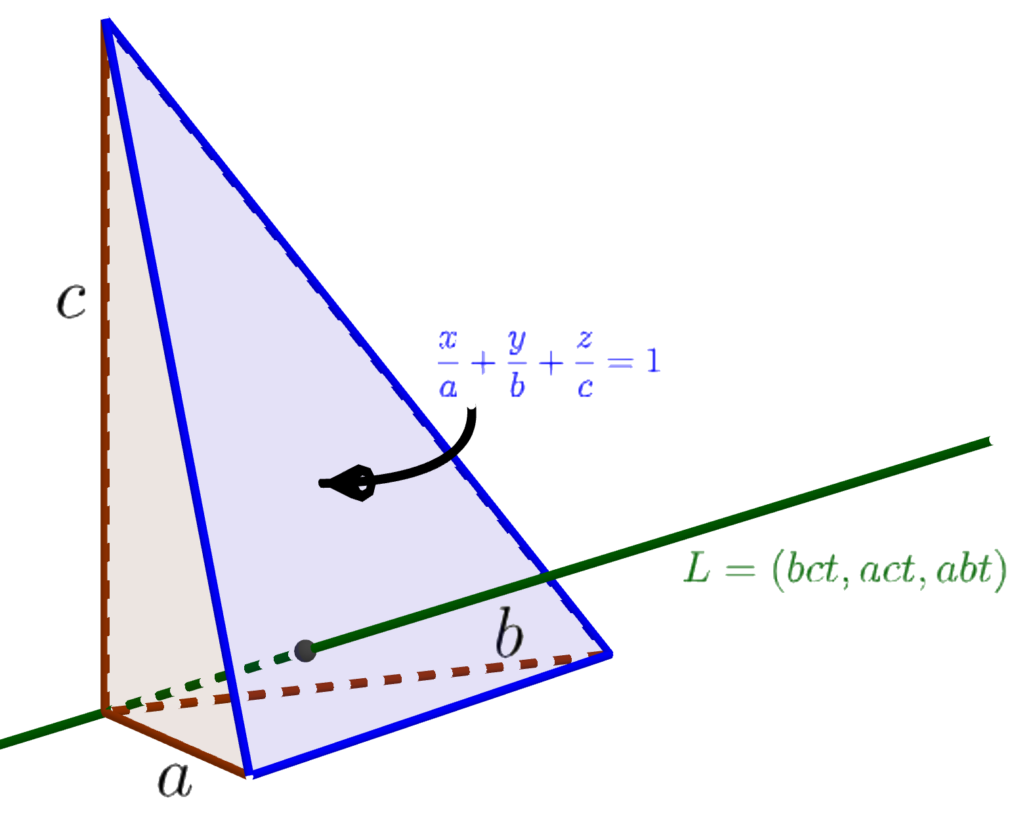
Place a right tetrahedron with legs $a$, $b$, and $c$ in a coordinate system so that its right-angled vertex is at the origin and the legs extend along the $x$, $y$, and $z$ axes, respectively. Then by the three-intercept form of a plane, the equation of the plane containing the base of the right tetrahedron is $x/a + y/b + z/c = 1$. (See the diagram to the right.) Also, the line through the origin given in parametric from with parameter $t$ by $(x,y,z) = (bct, act, abt)$ is perpendicular to the base (you can check this by taking the dot product of $(bc, ac, ab)$ with the two vectors $(a,-b,0)$ and $(0,b, -c)$ which both clearly lie in the plane of the base). This line intersects the plane at the point \[\left(\frac{a(bc)^2}{(bc)^2+(ac)^2+(ab)^2},\frac{b(ac)^2}{(bc)^2+(ac)^2+(ab)^2},\frac{c(ab)^2}{(bc)^2+(ac)^2+(ab)^2}\right).\] The line segment from the origin to this point has length $abc/\sqrt{(bc)^2+(ac)^2+(ab)^2}$ (that’s where I’m using the regular PT). But this line segment (dashed green in the diagram) is also an altitude of the tetrahedron to the base. Since the volume of the tetrahedron is $abc/6$, the area of the base must be $\frac12\sqrt{(bc)^2+(ac)^2+(ab)^2}$. So indeed the square of the area of the base is $(bc/2)^2 + (ac/2)^2 + (ab/2)^2$, which is the sum of the squares of the areas of the other three sides as desired.

In case you’re wondering, the Pythagorean Theorem does generalize in this way to $n$ dimensions: the square of the $(n-1)$-hypervolume of the base of a right $n$-simplex is the sum of the squares of $(n-1)$-hypervolumes of the other faces, and the exact same proof as just given, except with more variables and an $n!$ in place of “6,” works.