The Curvature of Hammocks
Hammocks often symbolize ease, relaxation and simplicity. Yet the mathematics of these structures contrasts with their seemingly effortless nature.

The image above shows a hammock in Quincy courtyard, captured on a Monday afternoon.
The particular Quincy courtyard hammock shown above consists of a rigid curved stand, and knotted netting attached to horizontal wooden bars. The wooden bars are in turn connected via more netting to hooks that hang on some fixed endpoints that are attached to the curved stand (or broader structure). Overall, hammocks can vary with regard to design (see the red hammock with an angular stand in the background), but the general structure of a membrane hanging between two rigid lines or points remains consistent.
Lying in this hammock, I started to wonder about the mathematical dynamics of the membrane supporting me. I became curious about two specific aspects of the hammock. One aspect is the natural curve of the hammock when it hangs in a resting static state without additional weight. The second aspect I am interested in is how that curve changes when the force of a body is added.
The underlying math of a hammock’s curve – both with and without added weight – are quite valuable to comprehend because they are reflected in other everyday structures such as arches and bridges. In this way, understanding the math of a smaller, everyday item such as a hammock can transfer to understanding the math of larger structures that carry more weight (literally and metaphorically) in society.
An initial glance at a hammock’s outline – viewing from a side perspective – reveals that there is an inherent curvature to the shape of an unloaded hammock at rest. To try to describe that shape geometrically, one could start by saying it resembles a crescent moon. When attempting to fit an equation to the curve formed by the hammock, however, it is important to take into account the nature of the membrane and the hammock’s construction. To begin, we can treat the curve as if it were two dimensional (later on we will ponder how the actual three dimensionality of the hammock could change the equation of the curve). From an initial glance, one might guess that the curve of a hammock is a parabola, with the equation y = cx2(where c is some constant). However, as it turns out, an undisturbed hammock actually takes on the form of a catenary curve, precisely because there is no added weight.
 A roughly side-on-view of the hammock, showing the 2D curve of the structure
A roughly side-on-view of the hammock, showing the 2D curve of the structure
A catenary curve is the curve of a hanging chain hanging under its own weight when supported at its ends. In contrast, a chain forms a parabolic curve when under a horizontally uniform load. Algebraically, a catenary curve is expressed by the equation y = acosh(x/a), where cosh is the hyperbolic cosine function. The diagram below shows the difference between a catenary and parabolic curve. While subtle, the parabola rises more quickly near the vertex, and more slowly farther away.
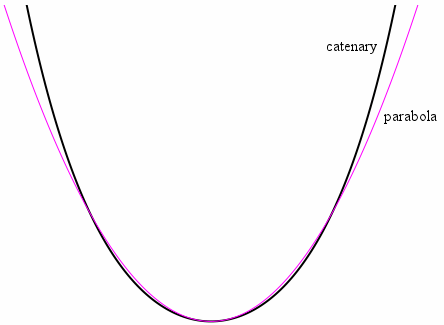
Visualization of a parabola and catenary – https://www.intmath.com/blog/mathematics/is-the-gateway-arch-a-parabola-4306
To better understand how this difference in curves occurs mathematically, we will explore how the equation for the catenary curve is derived:
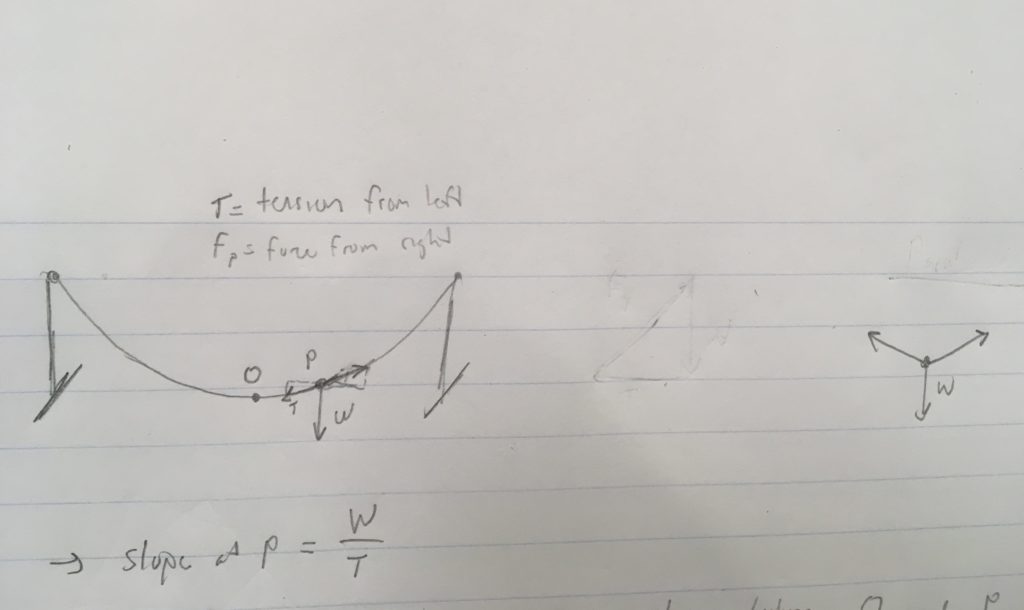
The weight (W) is proportional to length of the chain between O and P, so we need to determine the arc length of the chain.
Let: y = height of chain, µ = linear weight density, s = length chain between O and P

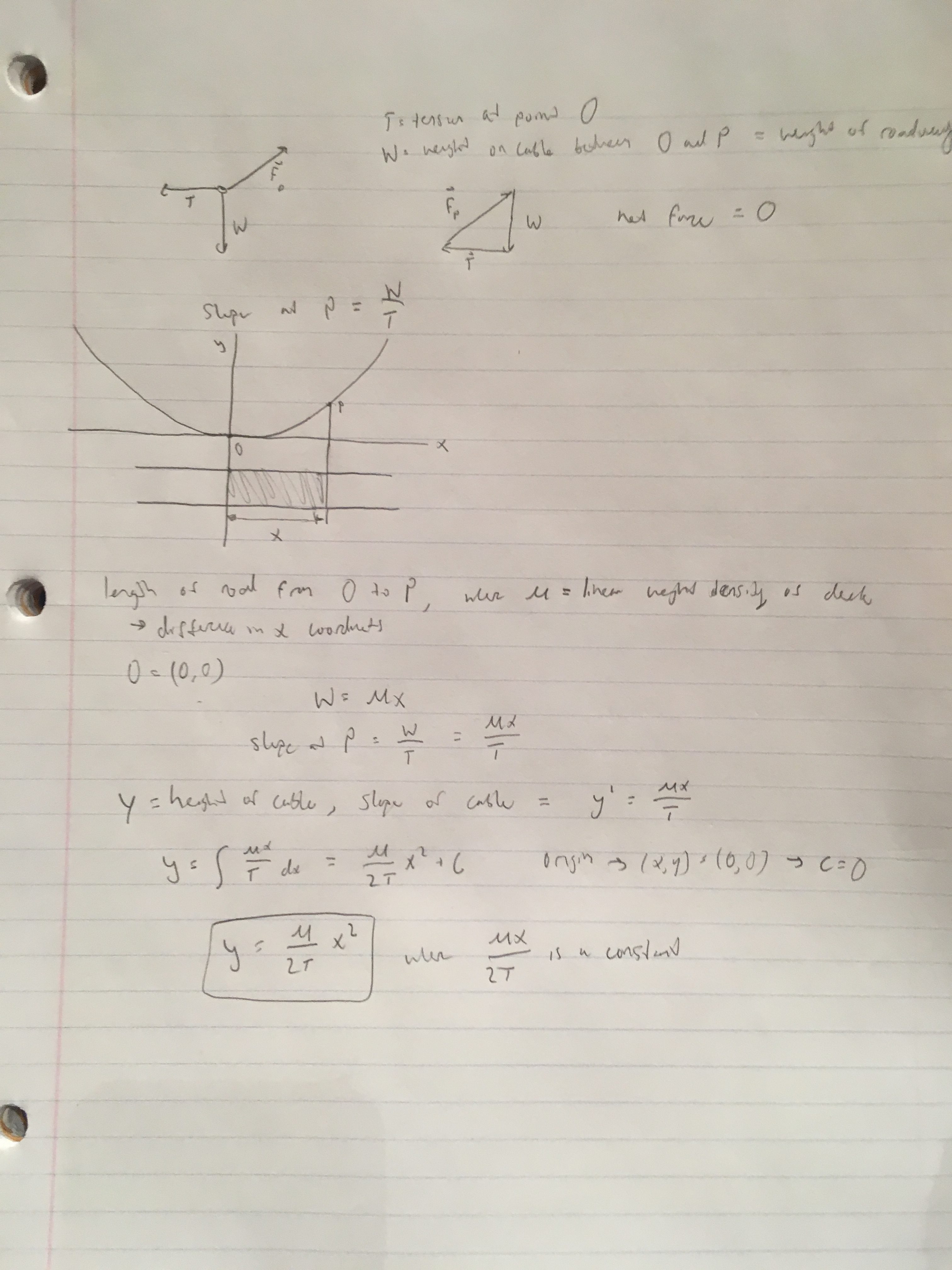
In contrast, for a parabolic curve (such as a suspended bridge with a roadway underneath), the weight of the roadway is evenly distributed and so the weight density is linear. Since the road is flat underneath, the length of the road between two points is the distance between the x coordinates. This linear distance reflects the arc length and in turn integrates to a quadratic function. See below the derivation of a parabola:
So far, we have relied on a two-dimensional approximation to model the hammock. This raises the question does the edge of an actual three-dimensional hammock actually form a catenary curve? Well, the catenary curve already exists in everyday life in other objects that span three dimensions. However, the paths in those objects are transversely rigid, and so the objects are constrained to be a projection of a two-dimensional curve. For example, there are simple suspension bridges (also known as catenary bridges) where the path follows the cable. There are also catenary arches, which are used to guide the placement of building materials. A hammock is uniquely different in that the center of a hammock hangs lower than the sides. As a result, we want to explore if that difference in hanging distorts the catenary along the sides or not.
We begin by capturing a picture of the hammock from a side-on view without any distortions based on the angle of the view. In this picture, we make sure that the two “endpoints” (locations where the netting meets the chain attached to the frame ) appear to be the same height. The lowest point is then horizontally midway between those two ends. We can calculate a catenary curve that goes through three points – the two endpoints at the same height and a minimum point halfway between those two endpoints. Unfortunately the original white hammock was not available at the time I took the picture, so I used the red hammock (which exhibits the same properties). The resulting catenary plot looks like this:

It is clear that the catenary curve is a great fit for the free hanging hammock. We can then move the curve to a different y intercept and see that it follows the edge of the hammock.

We can clearly visualize how the catenary curve applies to a hammock at rest in multiple locations (such as along the edge). This discovery leads to the conclusion to our original question that the edge of a three dimensional hammock does indeed form a catenary curve.
But hammocks are meant for – and much more enjoyable when – lying in them. How will a person’s added weight change the curve of a hammock? A hammock is meant to carry additional weight, and its membrane’s shape changes when weight is added. The material of the membrane is often flexible to accommodate the extra weight, which in turn causes the catenary curve to be elastic. However, with enough added weight, the initial catenary curve can lose it’s shape and can rearrange itself in space. One possible final formation is a parabolic curve.
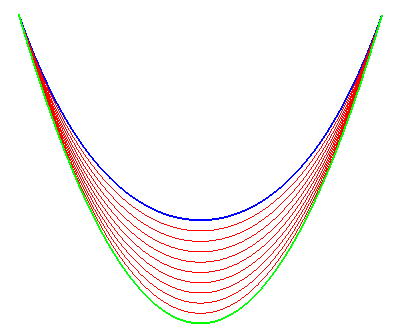
Elastic Catenary as it stretches: blue is the catenary and green is the parabola -https://www.mathcurve.com/courbes2d.gb/chainette/chainetteelastique.shtml
In this way, we can guess a hammock holding a person will form a parabola. Unfortunately, a person does not represent a horizontally uniform load, rather a person’s weight can be concentrated at his/her center of mass (slightly below the belly button). As a result, when someone rests in a hammock, the weight will be added to the middle region of the hammock netting (aligned with the body’s center of mass), causing the hammock to dip lower near the center. Unfortunately, there was not enough time to take measurements and run actual calculations to determine the shape of the curve of a hammock with a body resting in it. The calculations become even more complicated because a specific body’s weight and resting spot on the hammock can further affect the shape. There is much to be discovered, and understanding three-dimensional hanging membranes (and how they change shape with additional weight) is a subject of ongoing mathematical research.
To sum up, some may consider it counterproductive to think extensively about the mathematics behind the hammock, especially considering that the purpose of a hammock is to relax and ease the mind. However we should remember that taking a moment to contemplate the mathematics of a hammock can provide a new level of appreciation for the object that provides much needed support.
Resources and Acknowledgements:
Ferreol, Robert. Elastic Catenary. 2017. https://www.mathcurve.com/courbes2d.gb/chainette/chainetteelastique.shtml
Carlson, Stephan C. Catenary Mathematics. https://www.britannica.com/science/catenary
Kunkel, Paul. Hanging with Galileo. 2016. http://whistleralley.com/hanging/hanging.htm
http://mathworld.wolfram.com/Catenary.html
Gambino, Stephanie. Center of Mass of a Human. The Physics Factbook. 2006. https://hypertextbook.com/facts/2006/centerofmass.shtml

