The Behavior of Concrete Stripes and Lattices

Harvard’s new Smith Campus Center opened less than a month ago, and ever since then I’ve done most of my studying there. While the main Harvard Commons area is all brand-new wood and glass, the building’s main corridor is dominated by large, exposed concrete walls. While exiting the building one day, I noticed that these walls have a particular and peculiar design to them which consists of parallel lines and rows of holes spaced two feet apart. Below are a few pictures of the concrete that I took last week. These lines are either vertical, horizontal, or measured to be at 45 degrees.

My first question was why the walls has this pattern as opposed to just being flat concrete. After doing some research online, I found out that these “holes” are a by-product of the process of pouring the concrete. When a wall of concrete is poured, a mold must first be set up. If you simply pour the concrete in a box, however, due to the weight of the concrete and its inclination as a liquid to spread out, the concrete can break the mold and ruin the wall. In order to keep the mold together throughout the process, metal rods called “snap ties” are put through the mold. As seen in the picture below, they are supported in the middle of the mold by reinforcing bars, which are tied together in a square grid. This explains why the holes are in rows and columns instead of, say, a triangular grid. In order to be the most efficient, they are evenly spaced, except possibly near the end of the wall if there isn’t enough room. This can be seen in the first picture above. When the concrete is poured, the rods hold the walls of the mold together and resist the outward pressure of the wet concrete. Once the concrete has dried, a cone mechanism tying the rod to the mold can be snapped off, which frees the rod and leaves the hole (and explains why they are called snap ties).

The stripes, on the other hand, are likely intentional. According to this architecture article, the default is to use big sheets of plywood for the concrete mold, as shown above. Since the sheets are flat, they produce flat, concrete walls. However, a more stylistic approach is to make something called “board-formed concrete.” Instead of using just plywood, A plywood mold is made and then the inside of it is lined with wooden boards. Then, when the concrete dries, the imprint of the boards (and the lines between them) remain, giving the wall a cool pattern, which is the case in the Smith Center. The stripes I observed were likely either horizontal, vertical, or at 45 degrees because these cases make setting up the lining easiest and have the most symmetry. Since this extra lining of boards adds time to the construction process, it must have been a aesthetic rather than a practical decision.

Here we have two separate phenomenon going on: one practical and necessary for making the wall, and one aesthetic and optional. Yet together they form two objects very dear to mathematicians: points and lines.  The points themselves, since they are evenly spaced in rows, form an integer lattice. An integer lattice in 2d is simply the set of all points (x,y) in the Cartesian plane where x,y are integers. The lines on the wall naturally translate into lines on the cartesian plane, and the question that first arises is if these lines intersect lattice points. This problem, however, ends up not being very fruitful. If a line through the origin has irrational slope, it will not intersect any other lattice points. If it has rational slope p/q, it will intersect any lattice point that is a multiple of (q,p). (If you are interested in learning more about this question, this is a good source).

Initially, the walls did not so much cause me to wonder, but rather annoyed me. Since the holes  and the lines are products of unrelated processes, the lines did not align well with the lattice, giving the walls an aggravatingly irregular pattern. And it was less about the lines intersecting or not intersecting the holes, but rather how the area between the lines intersected the holes. That is, it felt natural to think of the area between two parallel lines as a “stripe” and see how many holes a stripe had in it. As you can see in the photos, some had none, some had one, and some had two or more.

The mathematical problem I came up with relating to this was: which stripes in an infinite integer lattice have to contain a lattice point? Which don’t?

It’s trivial that generally horizontal and vertical stripes don’t have to contain a lattice point (just place the line between two rows or columns of lattice points!). Note that to simplify calculations I will sometimes refer to a stripe’s “vertical width” instead of its width in the traditional sense. The vertical width the vertical distance between the two parallel lines determining it. Using some trigonometry, you can convert this vertical width to regular width as desired. Note that vertical width is undefined for vertical stripes (which will be okay since we will not be dealing with this case anyway) and that vertical width can often be misleadingly larger than regular width, particularly when a stripe’s angle approaches π/2.

A first significant observation I was able to come up with was that all stripes with irrational slope contain a lattice point. This follows from the fact that integer multiples of an irrational number modulo 1 are dense (by modulo 1, we mean we take only the decimal part of a number, and not the integer part, leaving the result between 0 and 1). A good proof of that fact is here. That is, if we take an irrational r and take the multiples of r: r, 2r, 3r, etc., there will always be one of these multiples between any two given numbers between 0 and 1. Because of this, if we set our stipe to be centered around a line y=rx+b with vertical width ε, at integer x-coordinates, the corresponding y-coordinates are dense in [b, 1+b] mod 1, which is the same as being dense in [0,1] mod 1. That is, there will always be an y-coordinate on the line within ε/2 of an integer, and thus the stripe will contain that lattice point.

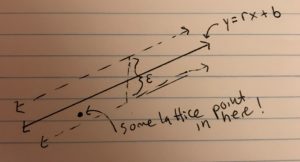
Now that we have covered the irrational slope case, we can look at rational slopes. As for the second result, given the line y=(p/q)x+b such that p/q is rational in lowest terms and if b is not an integer multiple of (1/q), there exists a stripe centered around the line that does not intersect any lattice points. For the proof of this, consider the set of y-coordinates of the line when x-coordinates are integers: p/q+b, 2p/q +b, 3p/q+b, etc. Note that we only care about these values mod 1, since this determines their vertical distance from a lattice point. In this list, once we get to q(p/q)+b= b (mod 1), the list starts over again. Thus, this list is finite mod 1. Moreover, since b is not an integer multiple of (1/s), none of these numbers are 0 mod 1. Thus, since each of these numbers is a finite, nonzero, vertical distance from a lattice point, there is a minimum vertical distance, and thus a stripe with vertical width shorter than double that minimum distance will not intersect any lattice points. We can convert the vertical width of that stripe to regular width.

If the y-intercept is rational, we can actually easily find this regular width (we use regular width in this case since we are going to find the closest lattice point to a line, and regular distance from a point to a line corresponds to the regular width that stripe can be.) The proof is influenced by this post and this post, both of  which give a similar method for finding the closest point to a line in a lattice. If the slope and y-intercept can be written as rational numbers, then the central line has an equation of the form ax+by+c=0, where a,b,c are integers. However, we are later going to want a,b to be coprime, so we are going to divide out any common factors, leaving us with a line with equation ax+by+(p/q)=0, where a,b,p,q are integers, a and b are coprime, and p/q is in lowest terms. Using the distance formula from line to point the distance from this line to a lattice point (s,t) is |as+bt+p/q|/√(a^2+b^2). Note that there’s a theorem in number theory called Bezout’s Theorem from which it follows that because a,b are coprime, there exists a linear combination of a,b that is equal to one (aka there exist integers n,m such that 1 = an+bm.) If we multiply both sides of this equation by any integer, we can get an integer combination of a,b that is equal to any integer (i.e. d=d(an+bm) =a(dn)+b(dm)). In particular, we want to find the lattice point (s,t) such that as+bt is as close as possible to -p/q (making the numerator of the distance formula above as small as possible). But for that we can simply make as+bt equal to the integer closest to -p/q, which then makes the numerator the distance from p/q to this closest integer, which is min(p/q mod 1, -p/q mod 1), where again mod 1 gives a decimal part between 0 and 1. Thus, the smallest distance between the line and a lattice point is min(p/q mod 1, -p/q mod 1)/√(a^2+b^2) (which should be nonzero according to the proof above), and thus any stripe with regular width less than twice this distance will not intersect any lattice points.

While I did not come up with or find a good way to get this distance when the y-intercept is irrational, the above method could be used to estimate or get some kind of bound on this (by estimating the y-intercept with a rational number). The Diophantine approximation can be used to find the best approximation of an irrational by a rational and also bounds its error.

Since the stripes I encountered in the Smith Center were either horizontal, vertical, or had a rational slope of 1 or -1, if we extended the lattice and stripes of these walls indefinitely it is possible that they contain stripes that do not intersect a lattice point. But as we saw above, just a small shift to an irrational slope guarantees all stripes contain a lattice point. I wouldn’t have guessed that something as mundane as concrete walls could lead me to such an interesting result.