Icosahedron in Octahedron
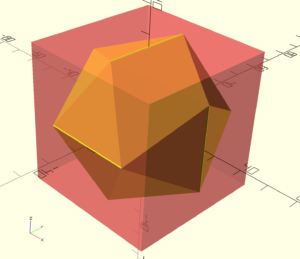
If you look again at the diagram of an icosahedron in a cube (at the right), you’ll see that because of its symmetry, all three of the icosahedron vertices nearest the top front cube vertex are the same distance from that cube vertex. That equidistance means that the body diagonal of the cube passes through the center of the icosahedron and is perpendicular to the nearest face of the icosahedron.
All of these properties hold at every vertex of the cube in relation to one of the eight faces of the icosahedron that do not have an edge lying in a face of the cube. Because the eight faces of the inscribed dual octahedron of the cube have these same properties, we’ve demonstrated that an icosahedron may also be inscribed in an octahedron like so:

It also means that if you extend the plane of one these particular eight faces of the icosahedron, it slices off an isosceles right triangular pyramid from the corner of the cube:

In a lattice of such cubes, eight of these pyramids fuse together at each vertex to create the octahedra seen inside the Anticos.

