Icosahedron in Cube
As mentioned and illustrated in the post on the Anticos, it’s possible to inscribe an icosahedron in a cube. (In this case, that technically means that given a cube, you can choose two points on each face of the cube such that the convex hull of the resulting set of twelve points is a regular icosahedron.)
But why should this be so? To see this, it’s easiest to start with a regular dodecahedron, say with unit edge length. Notice the interesting pattern of the blue face diagonals in this diagram:
 are enough to guarantee that the blue figure is precisely a cube.</p>
<p>Moreover, it’s also clear from the diagram that the red edges are parallel to the faces of this blue cube. (By the symmetries highlighted in the last paragraph, both endpoints of a red edge are the same distance from the nearest face plane of the cube.) Therefore, if we expanded the cube slightly, each red edge would lie in a face of the cube. In other words, a regular dodecahedron has a property very similar to the one we are looking for concerning the icosahedron. (Which begs the question of what the Antidodec would look like — an <strong>S∞</strong> project for another day!)</p>
<p>We want to transfer this property to the icosahedron. Now, the dodecahedron is the dual of the icosahedron. And one, perhaps slightly less well-known, way of passing from a regular polyhedron to its dual is to rotate each edge a quarter turn around the axis connecting its midpoint to the center of the polyhedron:</p>
<div class=)
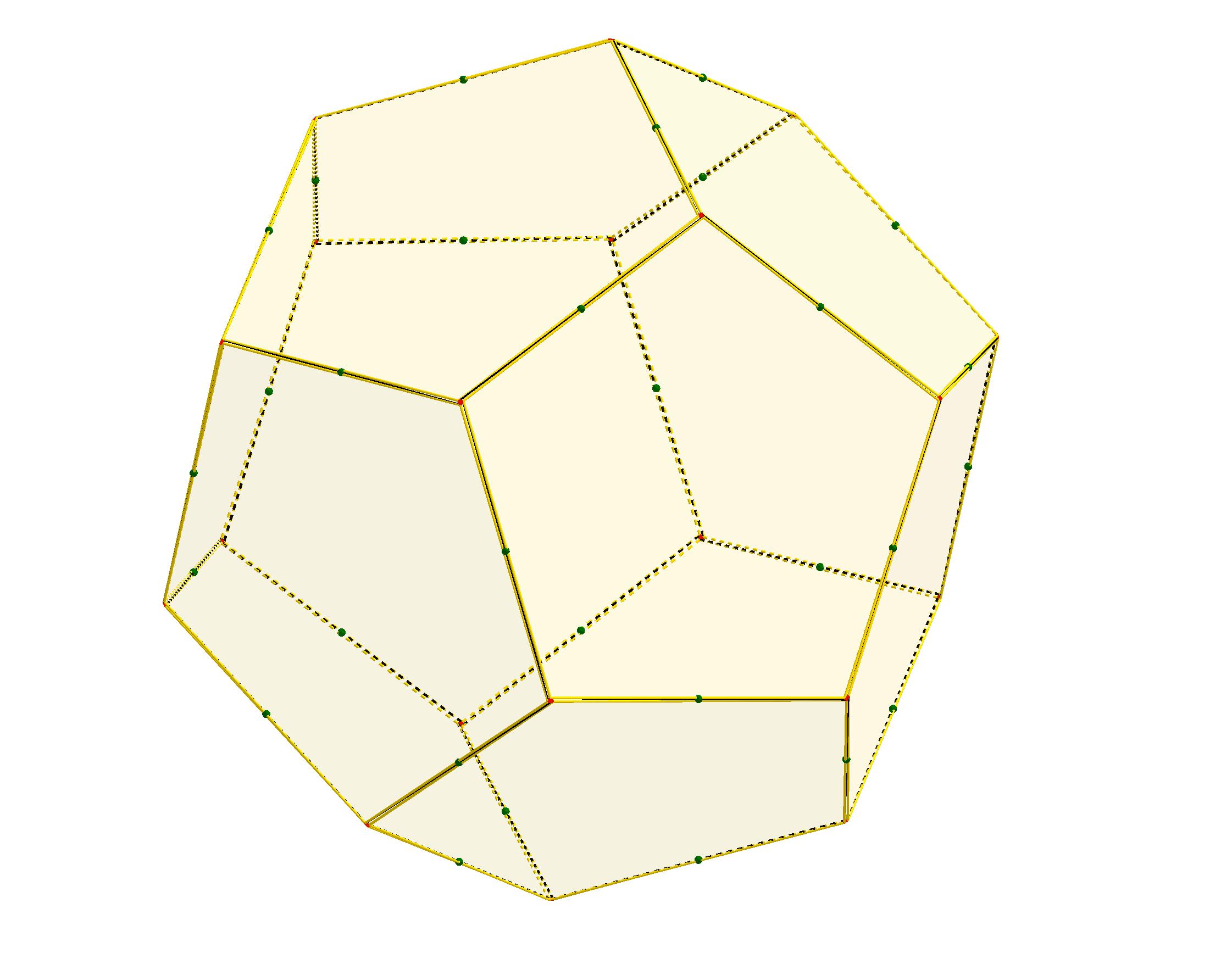
Notice that during this transformation, each of the edges remains in the plane perpendicular to that axis. Therefore, twelve of the vertices of an icosahedron lie on the surface of a cube, two on each face. Since an icosahedron only has twelve vertices, it is inscribed in a cube.