Balance of forces
As mentioned at the end of the last MathStream post, the actual shape that the six-strut tensegrity structure takes on is close to, but not quite precisely, a regular icosahedron. And that fact immediately makes you want to build a tensegrity structure that will under ideal circumstances assume the shape of a truly regular icosahedron. What would that entail? Why is the classic tensegrity not a regular icosahedron? One possibility that immediately comes to mind is that not all of the edges of the icosahedron are represented in the same physical way in the model. Namely, as you may recall from this diagram,
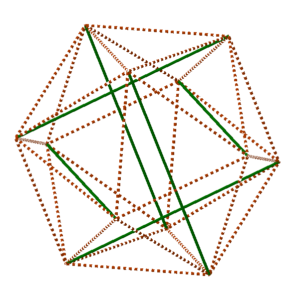
there is no rubber band lying along some of the edges of the icosahedron. To test if that’s the reason that the six-strut is not regular, we’d want a different arrangement of elements so that there will be exactly the same tension on a rubber-band connection between every closest pair of endpoints of the six struts, as shown in this diagram.
So, you might immediately start tying to build such a configuration. But that will bounce you right back to a mathematical question: how can we route the rubber bands so that there is exactly the same amount of rubber band between every closest-neighbor pair of endpoints? In fact, one of the wonderful things that happens at Studio Infinity is that many of the things we try to build lead to new mathematical questions, and many of the mathematical discoveries we encounter suggest new things to build. So the MakeStream and MathStream really build on each other.
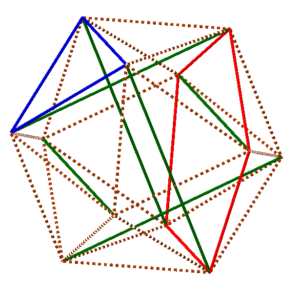
Getting back to the question at hand, it amounts to finding a route for each of several rubber bands so that the route of each band traverses the same number of edges of the icosahedron we are trying to achieve, and so that every edge is covered. Since the icosahedron has thirty edges, that immediately narrows down the possible number of rubber bands we might use. For example, there might be ten rubber bands each covering three edges, or six rubber bands each covering five edges, or five rubber bands each covering six edges, and so on. And since each rubber band is a loop, the edges covered will have to form a loop on the surface of the icosahedron. For example, there are fairly obvious loops one could make with three edges (in blue) or with five edges (in red) in this diagram.
So you can just start trying to cover the edges with loops of the same length. In fact, I recommend that you give it a try right now, maybe using the six-strut model you’ve made, or the diagram above. See if you can find a way to route rubber bands to cover every edge, so that every loop is the same length, before you read further.
After a while of trying, you may start to get discouraged. You might start to feel that this is an impossible task. And that would not be too surprising, because it is impossible. But when we make a statement like that in mathematics, we have to back it up. If you want to claim that something is impossible, you can’t just list the seventeen things you tried that didn’t work. You’ve got to find reasons why no possible routing of rubber bands, no matter how clever, will cover all of the edges and have every loop be the same length.
And the key to that in this case is even and odd. First count how many edges meet at every vertex: five, an odd number. Next count how many of those edges rubber bands can cover. Well, every rubber band is a loop, so it must arrive at the vertex by some edge, and then leave that vertex by a different edge. It might later come back to that vertex by yet another edge, but if so, it has to leave again by a still further edge, in order to form a single closed loop overall. So in short any one rubber band covers an even number of edges touching the vertex. And since the sum of a collection of even numbers is even, we can be sure that the rubber bands are covering an even number of edges touching the vertex.
And so now we run into the problem. An even number cannot be equal to an odd number, so we can’t possibly have covered all of the edges. So there in fact is no way to route the rubber bands as desired.
So we regretfully conclude that there is no way to construct the regular icosahedron we are looking for, right? Not quite. Another habit in mathematics is, when something doesn’t work out the way you thought it might, to see if there’s a way to change the assumptions so that it does work out. And in this case, there is something we can change: rather than providing the tension between two neighboring endpoints by virtue of a single segment of rubber band, why couldn’t there be exactly two different (but identical in length) segments of rubber band covering each edge? Then there would be ten different segments of rubber band reaching each vertex, which is an even number, and the contradiction underlying our impossibility argument would melt away in a puff of logic.
And now we can very pleasantly notice that there are exactly twelve of the five-edge pentagonal paths similar to the one highlighted in red in the last diagram above, and that each edge lies on exactly two of these pentagonal paths. So now the plan is simple: connect one rubber band along each pentagon, and the icosahedron should simply materialize from the balance of forces. Let’s return to the MakeStream to see if it works…