Ruler and Compass on a Sphere
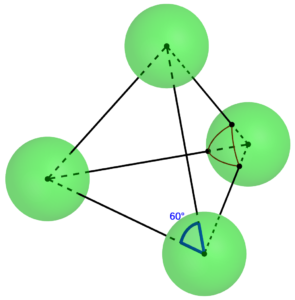 For this project, I needed to figure out (a) where should the holes be in spheres to connect them by straight lines to form a regular tetrahedron, and (b) how to locate those points on a physical sphere. The diagram makes part (a) fairly straightforward. We can see that the angle between any two holes (as viewed from the center of one of the spheres) should be 60°, the angle at each vertex of an equilateral triangle. And since 60° is one-sixth of a full circle (or an angle of τ/6, as the tauists point out), we can find the required distance d between any two holes on the surface of a sphere of radius r to be d = rτ/6, or approximately d ≈ 1.047r.
For this project, I needed to figure out (a) where should the holes be in spheres to connect them by straight lines to form a regular tetrahedron, and (b) how to locate those points on a physical sphere. The diagram makes part (a) fairly straightforward. We can see that the angle between any two holes (as viewed from the center of one of the spheres) should be 60°, the angle at each vertex of an equilateral triangle. And since 60° is one-sixth of a full circle (or an angle of τ/6, as the tauists point out), we can find the required distance d between any two holes on the surface of a sphere of radius r to be d = rτ/6, or approximately d ≈ 1.047r.
Now, how should we actually locate the points? As you can see from the diagram, they form a sort of “spherical equilateral triangle,” each point the same distance from each of the other two. And as you may recall, it’s pretty easy to construct an equilateral triangle in the plane. Fortunately, exactly the same procedure works on a sphere: First, select any two points a distance d apart on the sphere. Then using each of the two points as center, trace out a spherical circle with radius d on the surface of the sphere. (In practice, you only need a small section of each circle in the vicinity of where they’re going to intersect.) Each of the two points at which those two circles intersect represents one of the two possible locations for the third vertex of the desired triangle.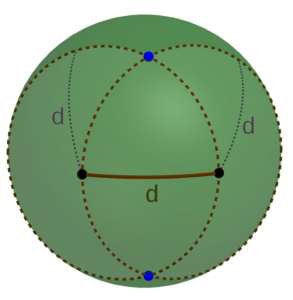
Moreover, it’s easy to perform this construction in practice. And mathematical curiosity makes us wonder: if it works for triangles, will it work for other constructions as well?

