So far, we’ve created a lot of interesting small models of tensegrity structures. However, for doing public programs of the sort Storm King Art Center was planning, it’s always helpful to be able to build much larger models of things. Building giant models seems to get the ideas across more vividly, engage visitors more thoroughly,… [Read more]
So why the interest in tensegrity here at Studio Infinity? It begins with Kenneth Snelson, the inventor of tensegrity (although perhaps not of the term) as a student of Buckminster Fuller. Ken went on to become a noted sculptor, using tensegrity in many of his works. One of those sculptures, Free Ride Home, resides at… [Read more]
When I set the goal of creating a new tensegrity structure for the Storm King Art Center workshop, I decided that I wanted to create a highly regular, symmetric structure, to contrast with the more free-form, organic style of Snelson’s Free Ride Home at the Center. (Snelson also created many very regular tensegrity sculptures himself.)… [Read more]
OK, so now we are going to try to force a tensegrity structure to take on the shape of a truly regular icosahedron. But we don’t have to search blindly for a way; we are armed with the results of this MathStream post about how to do it. To sum those results up, if we… [Read more]
As mentioned at the end of the last MathStream post, the actual shape that the six-strut tensegrity structure takes on is close to, but not quite precisely, a regular icosahedron. And that fact immediately makes you want to build a tensegrity structure that will under ideal circumstances assume the shape of a truly regular icosahedron.… [Read more]
So maybe you’ve made the classic six-strut tensegrity (or perhaps you’ve just looked at the pictures) and you’re wondering what shape that is, exactly. Naturally, since mathematics is among other things the science of shape and structure, understanding that is going to involve a little math. And in mathematics, sometimes it’s easiest to understand something… [Read more]
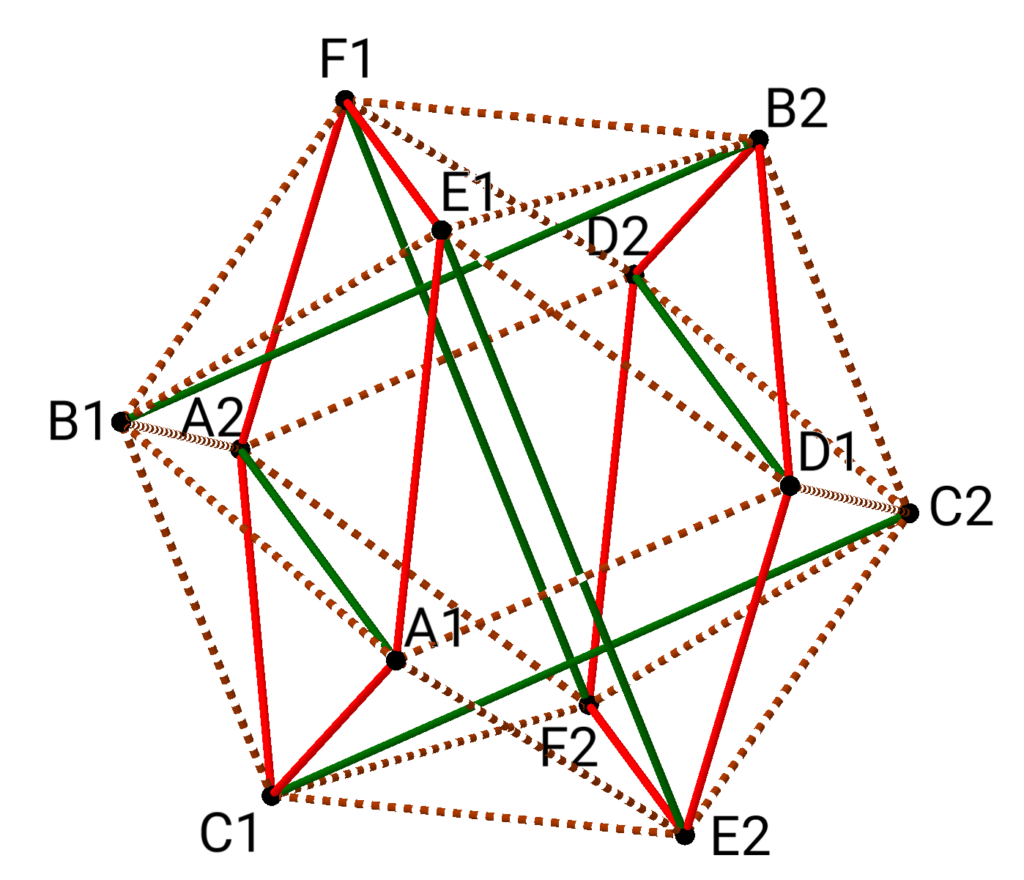
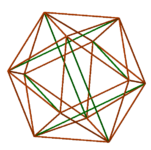
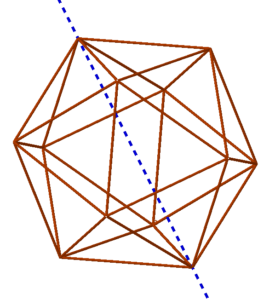
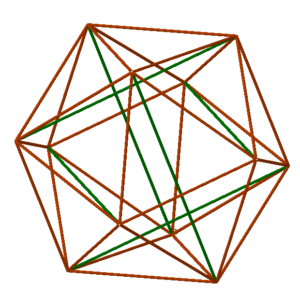
Studio Infinity is kicking off with a group of articles that feature the concept of tensegrity. What does that mean? A three-dimensional structure displays tensegrity if its compression members — rigid components that can hold their shape even when pushed inward by external forces — are connected only by tension members — materials that become… [Read more]